Calculating the Astronomical Unit
during a Transit of Mercury
using Satellite Data
Dr. Sten Odenwald (NASA/IMAGE)
Dr. Bart DePontieu (Lockheed Martin/TRACE)
Introduction to Triangulation:
Suppose you were trying to measure the width of a canyon from your side to the distant canyon wall. You couldn't pace the distance. Could you come up with a way to make this measurement safely?
Teacher Note: Have the class suggest ways that they could measure this distance.
Surveyors and geologists encounter this kind of problem measurement problem all the time. Over the course of centuries they have found a simple way to solve this problem. They use a method called 'triangulation'. Here's how it works:

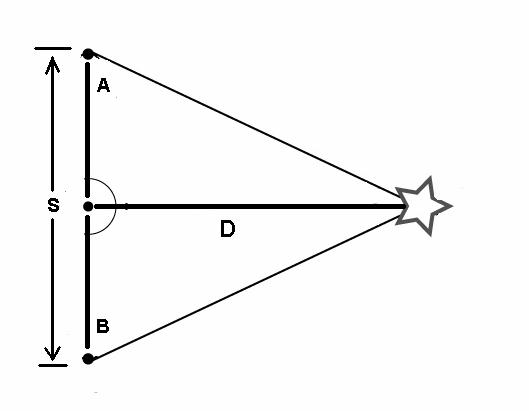
In ordinary land surveying, imagine a distant mountain peak (the star in the figure above) and two observers are located at 'A' and 'B' separated by a few miles (the length 'S'). The base angles at A and B can be measured with an instrument called a theodolite. By knowing the base distance A to B, and the baseline distance S, the distance to the peak can be worked out with a simple scaled drawing or with trigonometry.
Teacher Note: At this point, have the students measure the distance to some remote object in the school yard by using the above triangulation method. Here are some activities to consider:
Aurora Triangulation from PhotographsIMAGE satellite activity (Grades 7 - 9)
Introduction to Parallax.
Suppose it was hard for you to measure the two base angles in the triangulation method. This could easily happen if the object were so far away that your instrument could not accurately discern that these angles were different than 90 degrees. For example, if the object is 10 miles away, and your baseline is only 5 feet long, the two base angles would have a measure of 89.9946 degrees. This angle differs from 90 degrees by only 0.0044 degrees which equals 16 seconds of arc (there are 60 minutes or arc/degree x 60 seconds of arc/minute of arc = 3600 seconds of arc per degree!) This would be a very difficult angle to measure even with very expensive modern surveying equipment!
To solve this problem, astronomers don't bother measuring the base angles at all. Instead, they measure the vertex angle in the triangle. It turns out that this angle is very easily measured using photographic techniques. The method is called trigonometric parallax or just 'parallax' for short. Here's how it works:
Extend your arm in front of you, hold your thumb up, and alternately open and close your eyes. You will see your thumb's position move against the more distant background in front of you. Astronomers call this the parallax shift as the figure below illustrates:
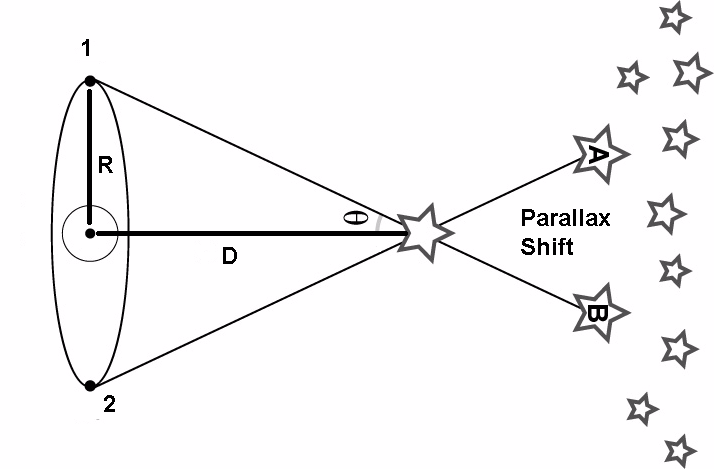
By knowing the distance between your eyes (2 x R) and how much this shift measures in degrees (twice the measure of the parallax angle
q ), you can calculate the distance to your thumb (D)! The formula that you use is:Tan (
q) = R / DBut this same principle applies to measuring distance to objects far away from you too...like the planets. Today, astronomers use photographs of stars taken 6 months apart. During that time, Earth has traveled from one side of its orbit to the other, and the orbit baseline is twice 93 million miles (150 million kilometers). By measuring how far the image of a star has shifted relative to the far more distant stars in the background between, say, January and June, astronomers can accurately measure angles as small as 0.001 seconds of arc or 0.0000003 degrees.
Believe it or not, long before the time when photography had been invented, astronomers were using the parallax technique to measure the distances to the nearby planets. By the time of Kepler in the early 1600s, astronomers knew exactly how far the planets were from the sun in terms of the distance from earth to Sun, but they didn't know exactly how many kilometers this distance equaled. Instead, they had a table that looked something like this:
|
Planetary Data ca 1620 |
||
|
Planet |
Year |
Distance |
|
Mercury |
0.24 |
0.38 |
|
Venus |
0.61 |
0.72 |
|
Earth |
1.00 |
1.00 |
|
Mars |
1.88 |
1.52 |
|
Jupiter |
11.86 |
5.20 |
|
Saturn |
29.56 |
9.54 |
When you make a scale model of the solar system with its nine planets, how do you know that in this model, the actual distance from Sun to Earth is 93 million miles and not, say, 153 million or 23 million? At the time of Kepler, the best estimates for this distance were as small as 5 million miles! The answer is that you have to come up with a way to actually measure this distance. Just like land surveyors surveying a distant canyon wall, you can't travel across distance to make this measurement.
Teacher Note: Ask the students to come up with ideas about how to measure the distances to the planets, without using modern technology or spacecraft.

In 1663, Rev. James Gregory who was an astronomer and mathematician considered, suggested that a more accurate measurement of the Earth-Sun distance could be made. He showed how this distance could be measured from observations of the transit of Venus made from various widely separate geographical locations. A few years later, Sir Edmund Halley, made the same suggestion in 1677, and published the details of this technique in 1716. Sir Edmund Halley described in detail how scientists from various nations could observe the upcoming 1761 and 1769 transits of Venus from many parts of the world. From the parallax shifts they would measure, they would be able to measure this distance from the Earth to Venus and the sun with near-perfect accuracy.
Teacher Note: Have students look up James Gregory and Edmund Halley and learn about what other things these two early astronomers were famous for. Note, also, that Gregory is seldom given any credit for his suggestion that the transit of Venus be used this way, while Halley is usually given all the credit. Ask students to explore this historical controversy and speculate why it may have happened.
The astronomical event called the transit of Venus happens because Venus orbits the sun inside the orbit of Earth. This means that every once in a while, Venus will pass across the face of the sun. The following photograph taken in 1882 by the U.S. Naval Observatory shows what this looks like. You can see Venus as a very large black spot directly above the center of the sun's disk. The other spots in the photograph are defects and blemishes in the glass photographic plate.

When these rare transit observations were made between 1761 and 1882, hundreds of scientists were involved in dozens of expeditions to the far corners of the world to set up sensitive equipment at a cost of millions of dollars. Some scientists actually died, or were arrested, in obtaining these measurements. Thanks to modern NASA space technology, we can re-do these transit of Venus parallax measurements very simply, so that students can get an idea of how parallax works. What we will do is to use NASA spacecraft data, instead of equipment on the ground.
Activity 1: TRACE observes the Transit of Mercury
The TRACE satellite orbits Earth and has its sensors trained on the surface of the Sun to search for solar flares. The changing perspective of the location of Mercury in its orbit also leads to a parallax shift. Here is a close-up of the consecutive images of Mercury as it traveled across the sun on May 7, 2003:

The composite shows the position of Mercury roughly every 450 seconds.
Teacher Note: By counting the number of exposures from peak to peak (about 13) students can calculate that the orbit period for this satellite is 13 x 450 seconds = 97.5 minutes, which is typical for satellites orbiting within a few hundred kilometers of earth's surface.
Method 1: Calculation using a Parallax Table
The first method we can use is to examine a table that lists the angular shift of the disk of Mercury at various times during the transit. At the moment that the satellite captured each image of Mercury in the montage above, it was also able to measure the vertical 'North-South' shift of the center of each image every 450 seconds. The Mercury Parallax Table shown below gives the times, and the angular shifts of the centers of each image in the sequence.
|
Mercury Parallax Data |
|||
|
Time |
Displacement |
Time |
Displacement |
|
5:19 |
+0.0010 |
7:19 |
+0.0038 |
|
5:27 |
+0.0025 |
7:27 |
+0.0010 |
|
5:34 |
+0.0045 |
7:34 |
+0.0004 |
|
5:42 |
+0.0035 |
7:42 |
-0.0013 |
|
5:49 |
+0.0023 |
7:49 |
-0.0032 |
|
5:57 |
+0.0011 |
7:57 |
-0.0039 |
|
6:04 |
-0.0013 |
8:04 |
-0.0043 |
|
6:12 |
-0.0025 |
8:12 |
-0.0024 |
|
6:19 |
-0.0035 |
8:19 |
-0.0010 |
|
6:27 |
-0.0044 |
8:27 |
+0.0015 |
|
6:34 |
-0.0024 |
8:34 |
+0.0025 |
|
6:42 |
-0.0011 |
8:42 |
+0.0045 |
|
6:49 |
+0.0015 |
8:49 |
+0.0035 |
|
6:57 |
+0.0028 |
8:57 |
+0.0025 |
|
7:04 |
+0.0046 |
9:04 |
+0.0010 |
|
7:12 |
+0.0038 |
9:12 |
+0.0000 |
Step 1..Have the students identify the largest positive (northward) and largest negative (southward) shift of the images. The answer should be +0.0046 and - 0.0044 degrees.
Step 2...Compute the difference between the largest positive and negative displacements to obtain the vertex angle. The answer should be 0.0046 - (-0.0044) = 0.0090 degrees.
Step 3...Determine the diameter of the TRACE orbit in kilometers as follows:
From the TRACE satellite orbit data at the time of the transit on May 9, 2003 the satellite was in a polar orbit (the red line in the figure below) with an altitude above Earth's surface of 580 kilometers.
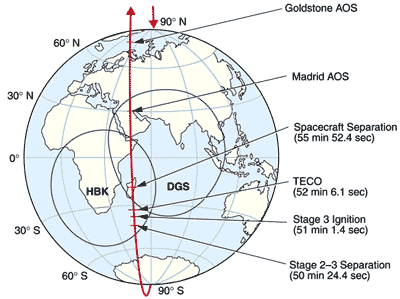
Adding the radius of the Earth (6378 kilometers) to this number (580 kilometers), we get an orbit radius
R = 6958 kilometers. We now know the orbit baseline for the TRACE Mercury parallax measurement.Teacher Note: The TRACE spacecraft has an orbit that changes its position throughout the year so that the plane of the orbit is always perpendicular to the line connecting the sun and earth. This allows the spacecraft solar panels to face the sun 24 hours a day and 365 days a year. It also lets the spacecraft keep a round-the-clock watch on the sun. At the time of the mercury transit, the orbit was inclined slightly from this perpendicular aspect so that the actual radius of the spacecraft orbit was R = 6,698 kilometers, and its diameter was 13,396 kilometers.
Step 4: Now that we have determined the vertex angle from Step 2 and the orbit radius, R, from Step 3, we can use the formula:
Tan (
q) = R / Dto determine the distance from Earth to Mercury (D). First, solve this equation for D:
D = R/Tan (
q)Remind the students that the vertex angle we measured in Step 2 (0.0090 degrees) is actually twice the parallax angle
q, so we must first divide the measured angle by 2.0 before using the formula.D = 6,958 km/ Tan(0.0045)
D = 6,958 km/ 0.0000785
D = 88.6 million kilometers
At the time of the transit on May 7, 2003, the distance between the Earth and Mercury was predicted to be 0.56 Astronomical Units. To find our estimate for the Astronomical Unit, we use the proportion: 1.0/L = 0.56/ D. Solving for L, this means that
L = 1.0 x 88.6 million / 0.56
L =
The actual value for the Astronomical Unit is 149.5 million kilometers!
Method 2: Parallax calculation using image analysis
We can also use the TRACE Mercury Transit image to determine the distance to Mercury. To do this, we first have to determine the scale of the print so we can measure the parallax angle
q.Procedure:
Step 1:
Print the TRACE image above on a separate piece of paper.Step 2: Cut the image out, and carefully tape it by its outer edge to a large sheet of paper. To give yourself room for Step 2, place the image above the center of the page, half way to its top edge.
Step 3: Through trial and error using a string, a tack and a pencil, draw a circle whose perimeter passes exactly across the edges of the solar disk shown in the picture. Measure the diameter of this solar circle in millimeters. A value near 200 millimeters is reasonable if you are working from the normal print version of the above image.
Step 4: At the time of the transit, the angular diameter of the sun is known by astronomers to be 0.53 degrees (1903 arcseconds) . Calculate the scale of the solar circle in degrees per millimeter by dividing 0.53 degrees by the measured diameter of the sun circle (210 millimeters) . Call this number 'A'. A value near 0.0025 degrees per millimeter is appropriate.
Teacher Note: Review with the students that a degree is split into 60 smaller divisions called arc minutes, and each arc minute is divided into 60 intervals called arc seconds. This should be familiar to the students from geography class and map reading. Have students convert from decimal degrees to arcminutes and arcseconds by doing a set of practice problems like the following:
1) 0.029 degrees = _________ arcminutes or ___________ arcseconds.
Answer: 0.029 degrees x 60 arcminutes/degree = 1.74 arcminutes
and 1.74 arcminutes = 1.74 x 60 arcseconds/arcminutes = 104.4 arcseconds.
Skip to Step 6 below
Alternate Method:
A simpler, though less accurate, method is to use the astronomical fact that the diameter of Mercury in this image is 0.0033 degrees (
12 arcseconds) , and use this to calculate the scale of this image.Step 1: Print the TRACE image on a piece of paper. A typical size of the image would be about 85mm x 203 mm.
Step 2: Measure the diameter of five of the Mercury disks with a millimeter ruler. For the above image size, a typical measurement series would be 1.2, 1.3, 1.3, 1.2, 1.0.
Teacher Note: The edges of the Mercury disk vary in sharpness and quality. Have the students make note of their experiences measuring Mercury's disk diameter. This is the major source of error in determining the scale of the print. You may want to compare the difficulty of this method with the first method where you measured the diameter of the sun. It is far easier to measure accurately a distance of 200 millimeters for the solar diameter, than it is to measure 1.2 millimeters for the diameter of Mercury. An uncertainty of reading the ruler to 0.2 millimeters in the solar diameter case is only an uncertainty of (0.2/200) x 100% = 0.1%, while for the mercury diameter it is a whopping (0.2/1.2)x100% = 17%.
Step 3:
Average these numbers to get the average diameter of Mercury on the print, 'D'. For the measurements listed in Step 2 yields 1.2 millimeters.Step 4: Calculate the scale of the photograph by dividing the angular diameter of mercury (0.0033 degrees) by its measured diameter (1.2 millimeters). For the example above, A = 0.0033/1.2 = 0.0027 degrees per millimeter.
Teacher note: This is a bit less precise that Method 1 because the diameter of Mercury on the print is such a small number of millimeters and is more inconvenient for students to measure than the much larger diameter of the Sun.
Step 5:
If we combine the answers from the two methods, we get an average value of (0.0025 + 0.0027)/2 = 0.0026 degrees/mm. For this exercise, we will use this average value.Step 6: Notice that the track of Mercury's images across the sun is a wavy curve. Draw a line through the centers of the highest disks of the Mercury image trace. Draw a second line through the centers of the lowest disks in the Mercury track.
Step 7: Use a millimeter ruler to measure the separation between these two lines. Call this number 'S'. Make several measurements along the two parallel lines just in case they are tilted. In the above example, a value near 2.0 millimeters was obtained. Values from 1.7 to 2.3 millimeters are also reasonable, but students should try to measure the separations to better then 0.5 millimeters and average the data using at least 9 points.
Teacher note: Measuring 9 points along the two 'parallel' lines will reduce the measurement error in the final averaged number to about 0.5/3 = 0.15 millimeters.
Step 8:
Calculate the vertex angle, P, in degrees by using the formula P = A x S. In the example, P = (2.0 mm) x (0.0026 deg/mm) = 0.0052 degrees. In the diagram for the parallax geometry, the vertex angle, P, is twice as large as the parallax angle q so that q = 0.0026 degrees.Notice that by using this photographic method, we can determine the measure of the vertex angle (and the parallax angle) to an accuracy far better than any mechanical measuring device (protractor, theodolite, surveyor's transit). This is how astronomers can measure such incredibly small angles!
Teacher note: Students should keep careful track of the difference between the vertex angle P and the parallax angle
q because of the factor-of-two difference in their geometric definitions.Step 9:
The TRACE satellite obtained the Mercury images by first shifting the solar disk image to the center of the picture frame, then taking the 'picture'. Since the solar image was re-centered each time, this solar parallax was subtracted from the full parallax angle we need to measure. To recover this 'instrumental effect' in the data, you have to add back the 0.0019 degrees for the spacecraft repointing, to the parallax angle you measured on the image. The full Mercury parallax angle q is then 0.0026 + 0.0019 = 0.0045 degrees.Teacher note: Explain to students that scientists always have to examine the details of how data is often taken in order to determine how their instruments alter the data. This process is called 'Calibration', and is very similar to what we have to do with our bathroom weight scales every once in a while. We have to make a slight change in the scale so that it registers 'zero pounds' when no one is standing on it. Ask students to identify other examples of the calibration process in other instruments they use to measure with.
Step 10:
The distance between the Earth and Mercury which produces this measured parallax shift can be computed from:Tan (
q) = R / DFrom the example where the parallax angle
q = 0.0045 degrees, we get a distance from Earth to Mercury, ofD = 6,958 km / Tan (0.0045)
D = 6,958 km / (0.000078)
D = 89.2 million kilometers.
Teacher note: If we use the more accurate estimate of the TRACE orbit diameter of 6,698 kilometers described in an earlier Step,
D = 6,698 km / Tan (0.0045)
D = 6,698 km / (0.000078)
D = 85.8 million kilometers.
5) At the time of the transit on May 7, 2003, the distance between the Earth and Mercury was predicted to be 0.56 AU. To find our estimate for the Astronomical Unit, we use the proportion:
1.0/L = 0.56/
This means that L = 1.0 x (
89.2 million / 0.56) so that L = 159.3 million kilometers.Teacher note: The actual value for the Astronomical Unit is 149.5 million kilometers!
Here is a table of the historical measurements of the distance from the Earth to the Sun since the time of Ptolemy. How well did your student's estimate stand up?
|
Table of Earth-Sun Distance Estimates using Parallax Method |
|||
|
Name |
Date (A.D) |
Value (miles) |
Method |
|
Hipparchos |
130 |
5 million |
Earth shadow on Moon |
|
Cassini |
1672 |
98 million |
Mars parallax |
|
Various |
1761 |
109 million |
Transit of Venus |
|
Various |
1769 |
88 million |
Transit of Venus |
|
Foucault |
1862 |
92 million |
Speed of Light |
|
Hall |
1862 |
92 million |
Parallax of Mars |
|
Stone |
1862 |
92 million |
Parallax of Mars |
|
Various |
1874 |
91.7 million |
Transit of Venus |
|
Houzeau |
1882 |
92.7 million |
Transit of Venus |
|
Harkness |
1889 |
92,797,000 |
Transits of Venus 1761-1882 |
|
Jones |
1941 |
91,500,000 |
Parallax of asteroid Eros |
|
Various |
1960 |
92,670,000 |
Motion of Pioneer 5 satellite |
|
NASA/JPL |
1961 |
92,955,820 |
Radar echo from Venus |
Congratulations! You have mastered the method for analyzing the transit of Mercury. As you can see, it requires many individual steps to get to an answer, and each student will end up with a slightly different answer. This raises some interesting issues that are worth exploring.
Extra Credit Problem 1: Have the students construct a histogram of the estimates, or an ordered series from which the mean, median and mode can be determined.
Extra Credit Problem 2: Have the students write down all of the steps and measurements that were required to make their estimate, and write in their journals which of these steps had the most uncertainty.
Extra Credit Problem 3: Have the students quantify what the amount of uncertainty is at each step by giving a range of alternate values that could have resulted from the various measurements.
Extra Credit Problem 4: Have the students assess whether the spread of the histogram in Problem 1 comes mostly from their measurement uncertainties in Problem 3.
Your next challenge will be to apply this same method to the transit of Venus which will happen on June 8, 2003!
Look at the following page, and fill-in all the missing 'TBDs' :
Calculating the Astronomical Unit During a Transit of Venus Using Satellite Data.Acknowledgment:
The Transition Region and Coronal Explorer, TRACE, is a mission of the Stanford-Lockheed Institute for Space Research, and part of the NASA Small Explorer program.
Comments:
http://canopy.lmsal.com/schryver/Public/TRACE/TRACEpodarchive17.html
This composite shows the transit of Mercury (4800 km diameter) across the solar disk, as observed by TRACE in its 1600Å pass band on 7 May 2003. The composite shows the position of Mercury roughly every 450 seconds.